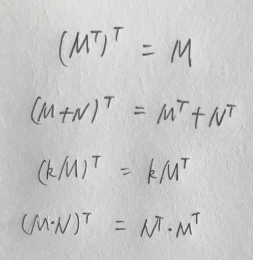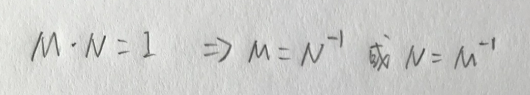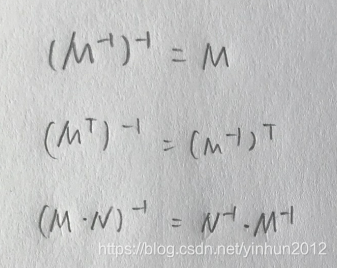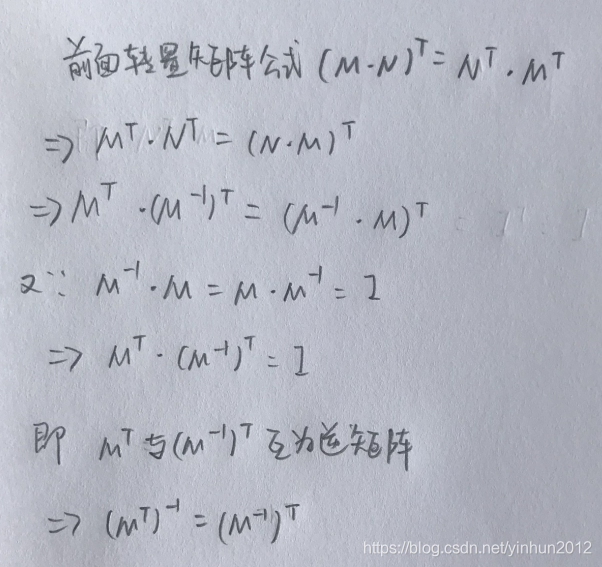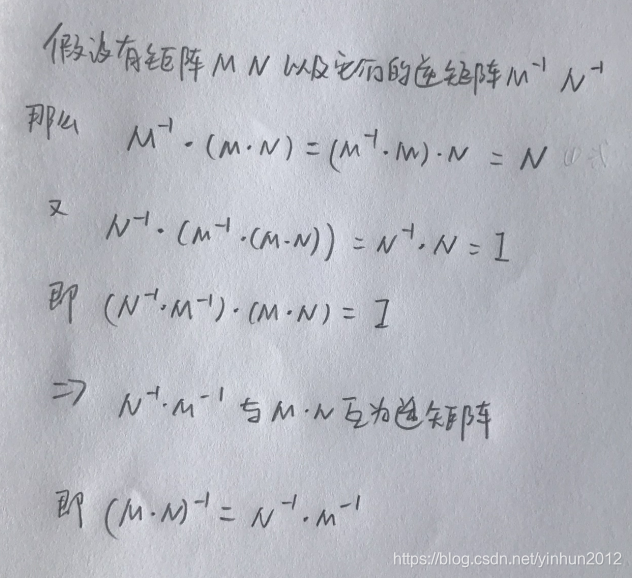Transformation

Games 101 Transformation

矩阵知识复习

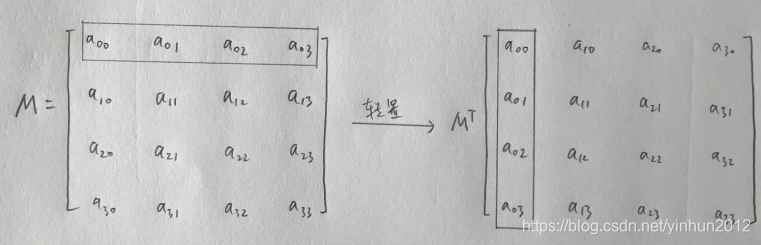
矩阵的转置

逆矩阵

存在矩阵M以及矩阵N，假如M*N = 矩阵I（Identify Matrix单位矩阵），那么矩阵M和矩阵N互为逆矩阵。

第二个解释

第三个解释

正交矩阵

矩阵的逆等于矩阵的转置

在三维变换中

旋转（a）角度和旋转（-a）角度是互逆的操作

旋转里，矩阵的逆等于旋转矩阵的转置

在旋转里 旋转矩阵的逆等与往相反的方向旋转相同的角度

先线性变换 再平移

欧拉角（Euler angle）

指的是绕参考坐标系主轴（x,y,z x , y , z ）之一旋转的角度。 也就是说，若新的坐标系是绕旧的坐标系的主轴（x,y,z x , y , z ）之一旋转形成的，那么这个旋转角就是欧拉角

Transformation

罗德里格斯公式

同二维坐标一样 先平移 再变换再平移回来

View / Camera Transformationzzz

Projection transformaion

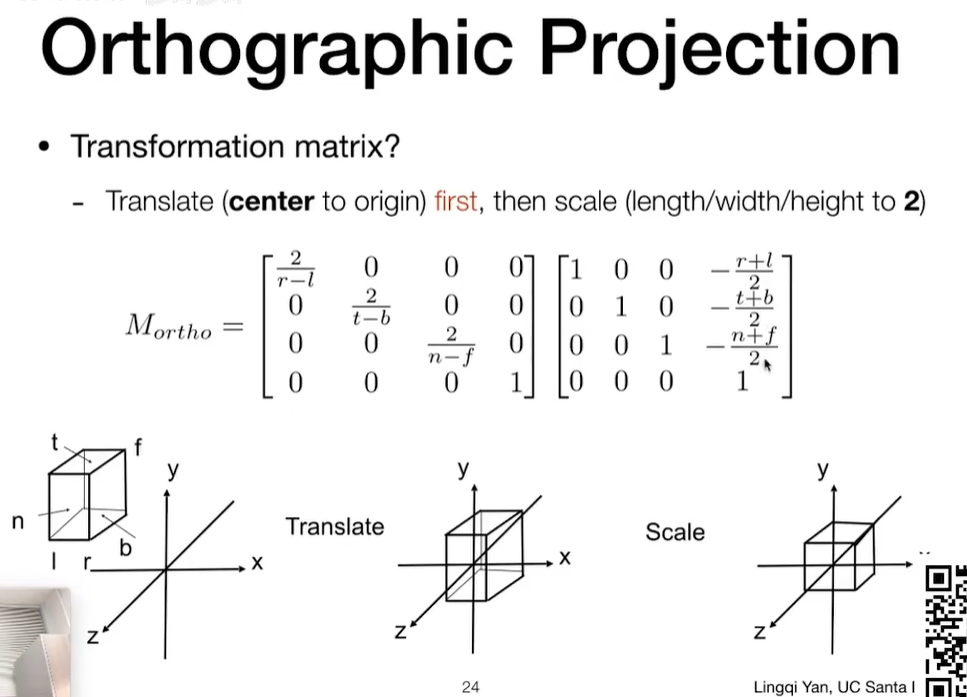
Orthographic projection 正交投影

工程制图

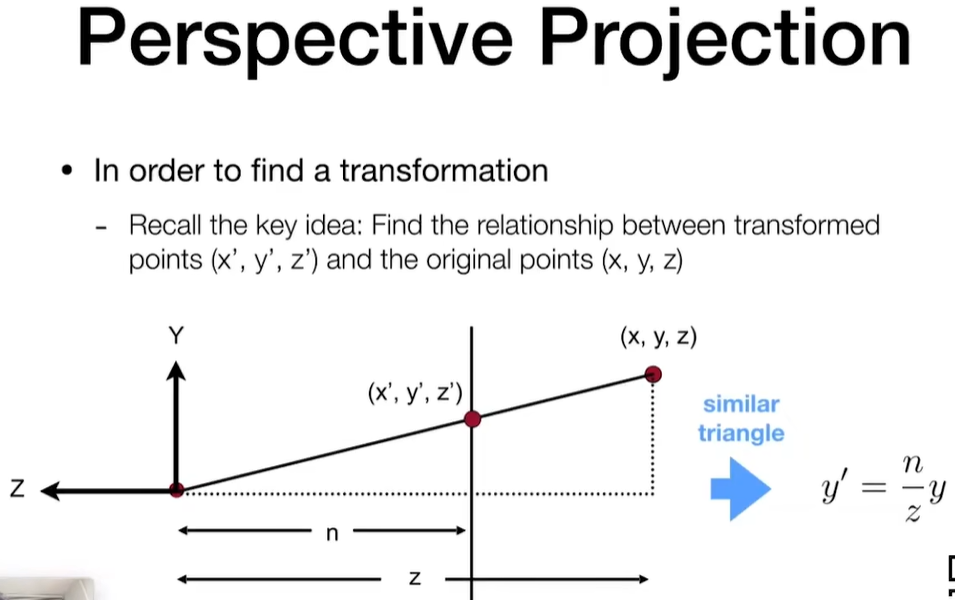
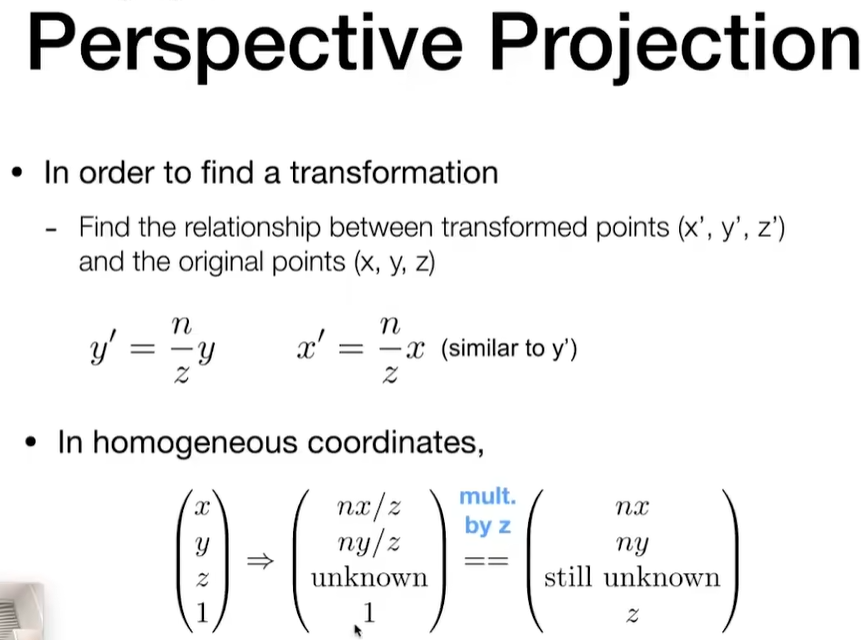
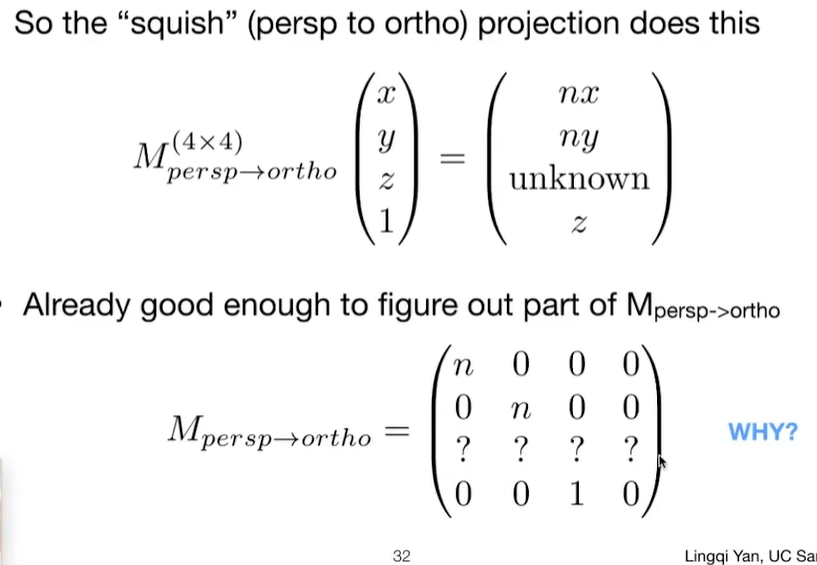
Perspective Projection 透视投影

cuboid 长方体 canonical 正则 规范 frustum 棱锥

最常用

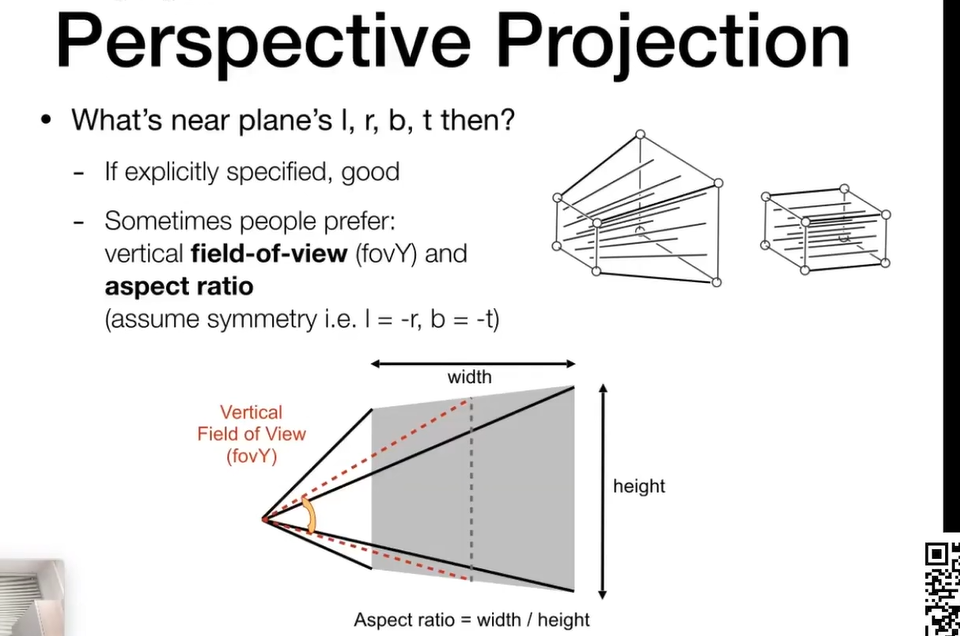
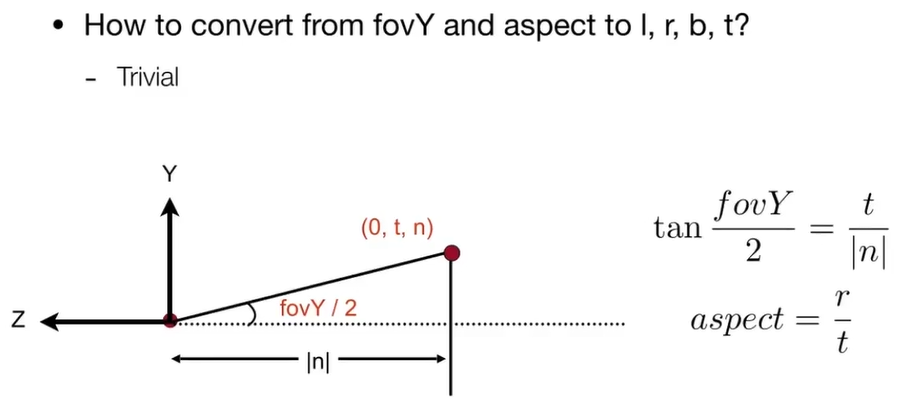
aspect ration 长宽比

vertical field of view (fovY) 垂直可视角度

assymetry n对称性

如何定义一个视锥 ———>只需要一个可视角度 和一个宽高比 还有n

Canonical Cube（规范立方体） to Screen

宽高比 1280*720（720P） 1920 * 1080（1080P）

引用：

https://blog.csdn.net/yinhun2012/article/details/84236202