Rasterization

Games101 Rasterization

For Your Information（FYI），可以看作一个整体

三角形： 最基本的多边形

只能是一个平面 比如四边形可以对折成为两个三角形成为不同平面 三角形不可以 除非变成两个三角形

明确简单的内部 可以判断一个点是否在三角形内

bayer patten

Jaggies 锯齿 Aliasing （Jaggies）走样 混淆 锯齿

采样（Sampling）是一个关键概念，用于将连续的信号或数据转换为离散的信号或数据。采样通常用于图像处理、渲染、纹理映射和抗锯齿等领域。

采样的基本概念
采样点（Sample Point）：在一个连续的信号或图像中选取的离散点。这些点用于近似表示原始信号。
采样率（Sampling Rate）：每单位长度（时间、空间等）上采样点的数量。较高的采样率通常能更精确地表示原始信号。
Nyquist 频率：为了避免混叠（aliasing），采样率必须至少是信号最高频率的两倍，这个频率称为 Nyquist 频率。
采样在图形学中的应用
图像采样：将连续的图像信号转换为离散的像素点。每个像素点表示图像中一个小区域的颜色和亮度信息。
纹理映射（Texture Mapping）：在三维渲染中，将二维图像（纹理）映射到三维模型的表面。纹理坐标通常在渲染过程中进行采样，以获取正确的纹理颜色。
抗锯齿（Antialiasing）：在渲染图像时，通过增加采样点或使用过滤技术，减少锯齿状边缘的出现，提高图像质量。

Rasterization — Antialiasing and Z-Buffering (反走样和深度缓冲)

• Viewing

view + projection + viewport （视口）

viewport：将（-1到1的三次方）的空间映射到屏幕上面

• Rasterization triangles

point - in - triangle test

Aliasing

Artifacts 瑕疵 图形学中看起来有问题的地方

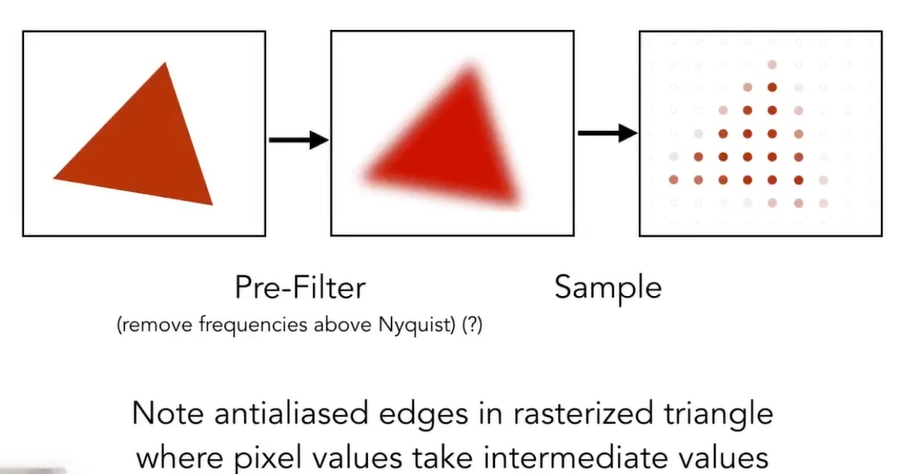
Antialiasing Idea ：Blurring （Pre-Filtering）Before Sampling 在采样之前做一个模糊或者滤波

不能先采样再做模糊 这种交blurred Aliasing

Frequency Domain （频域）

Frequency

Fourier Transform 傅里叶级数展开

傅里叶变换和逆傅里叶变换

Aliases 走样: 同样的方法采样两种函数 我们没有办法去做区分

Filtering 滤波 = Getting rid of certain frequency contents 抹掉 特定的频率

傅里叶变换可以把一个函数从时域（空间上 不同的位置也算时域）变成频域

这张图片展示了图像的频率内容，通过傅里叶变换将左边的时域图像转换为右边的频域图像。让我们详细解释一下低频和高频信号以及中间的两条线。

时域图像

• 左图：这是原始的时域图像，即我们在显示器上看到的普通图像。在这个图像中，亮度值随着图像的空间位置变化。

频域图像

• 右图：这是通过傅里叶变换得到的频域图像，显示了原始图像中的频率成分。

低频信号

• 低频信号：在频域图像的中心区域，表示图像中变化缓慢、平滑的部分，例如大面积的相似颜色区域或缓慢变化的光照。
• 解释：图像中心的亮点代表了图像中的低频成分。越靠近中心的点，表示的频率越低。

高频信号

• 高频信号：在频域图像的边缘区域，表示图像中变化剧烈、细节丰富的部分，例如边缘、纹理和噪声。
• 解释：图像边缘或远离中心的亮点代表了图像中的高频成分。越远离中心的点，表示的频率越高。

中间的两条线

• 水平和垂直线：这些线表示图像中的水平和垂直方向的频率成分。它们可能是由于图像中的某些对称结构或周期性变化造成的。
• 解释：中间的两条线通常是由于图像中存在大量水平和垂直的边缘或纹理。它们在傅里叶变换中表现为沿水平方向和垂直方向的显著频率成分。

频域图像解释

• 中心亮点：图像的平均亮度或直流成分（DC Component）。
• 环状结构：表示图像中具有各个方向的频率成分。如果图像中存在圆形或环形对称的纹理，这些纹理的频率成分会在频域图像中表现为环状结构。
• 亮度和对比度：频域图像中亮度较高的区域表示对应频率成分的能量较高，也就是说在原始图像中这些频率成分的变化幅度较大。

Conclude

• 左边的时域图像展示了实际图像内容。
• 右边的频域图像展示了图像中不同频率成分的能量分布。
• 中心区域表示低频信号，边缘区域表示高频信号。
• 中间的水平和垂直线表示图像中的水平和垂直方向的频率成分。

通过理解频域图像，我们可以更好地分析图像的特征，例如图像的纹理、边缘和噪声，从而在图像处理、压缩和分析中应用这些知识。

抹掉低频信号

高通滤波 ：通过一种滤波器 只有高频信号可以通过

只留下低频信息

去掉高频和低频信息

滤波 Filtering 去掉一定频率的信息

Filtering = Convolution 卷积（Averaging 平均）

时域的卷积等于频域的乘积

如何卷积 1. 可以直接用图做卷积操作 2. 也可以把这个图通过傅里叶变换变换到频域上 把卷积的滤波器变到频域上 两者相乘后得到频域的结果 再通过逆傅里叶变换得到时域上的结果

这里的这个滤波器 Box Function 实际上是 Low Pass Filter 低频滤波器

越大的box越模糊

Sampling = Repeating Frequency Content 采样：重复频域（频率）上的内容

（C）是冲击函数 只在这个位置上有值 在其他位置上没有值

走样（Aliasing）：频率的频谱在经历复制粘贴或者搬移的情况下发生了混合

如何反走样

1.Increase sampling rate 增加采样率

2.把高频信息拿掉 先模糊再采样

Antialiasing By Supersampling （MSAA）

No free Lunch！

What’s the cost of MSAA

• FXAA fast Apptoximate AA

得到带锯齿的图形 替换掉边界

• TAA Temporal AA

复用上一帧感知到的结果

Super resolution / super sampling